
Равнобедренному треугольнику присущи общие характеристики треугольников. Но он обладает и рядом особенностей. Вычислить базовые параметры этой фигуры помогут формулы.
Равнобедренный треугольник — одна из разновидностей этих геометрических фигур. Площадь, периметр и основание такого треугольника вычисляют по особым формулам.
Треугольники представляют собой трёхсторонние многоугольники. У них все три стороны могут быть равными (равносторонние) или разными (разносторонние), могут быть равны только две стороны. Стороны могут находиться под разными углами друг к другу, в том числе под прямым углом 90°, тогда такие фигуры называются прямоугольными треугольниками.
Что такое равнобедренный треугольник? Это треугольник, у которого две стороны одинаковой длины, а третья больше или меньше их. Две равные стороны называются боковыми, третья — основание. Частным случаем равнобедренного треугольника считают правильный равносторонний треугольник, в котором боковые стороны и основание равны.
Угол между боковыми сторонами такого треугольника называется вершинным углом. Два угла между боковыми сторонами и основанием называются углами при основании. Эти углы, лежащие против равных боковых сторон равнобедренного треугольника, равны.

Равнобедренный треугольник, как утверждает крупнейший в мире издатель образовательных ресурсов Twinkl, имеет только одну ось симметрии. Это линия из вершинного угла до середины основания. Она делит равнобедренный треугольник на два равных треугольника. При этом ось симметрии совпадает с:
Из этих особенностей треугольника можно сделать вывод о его признаках: если два угла треугольника равны, если совпадают биссектриса, медиана и высота, то это равнобедренный треугольник.
Свойства равнобедренного треугольника определены в четырёх теоремах:
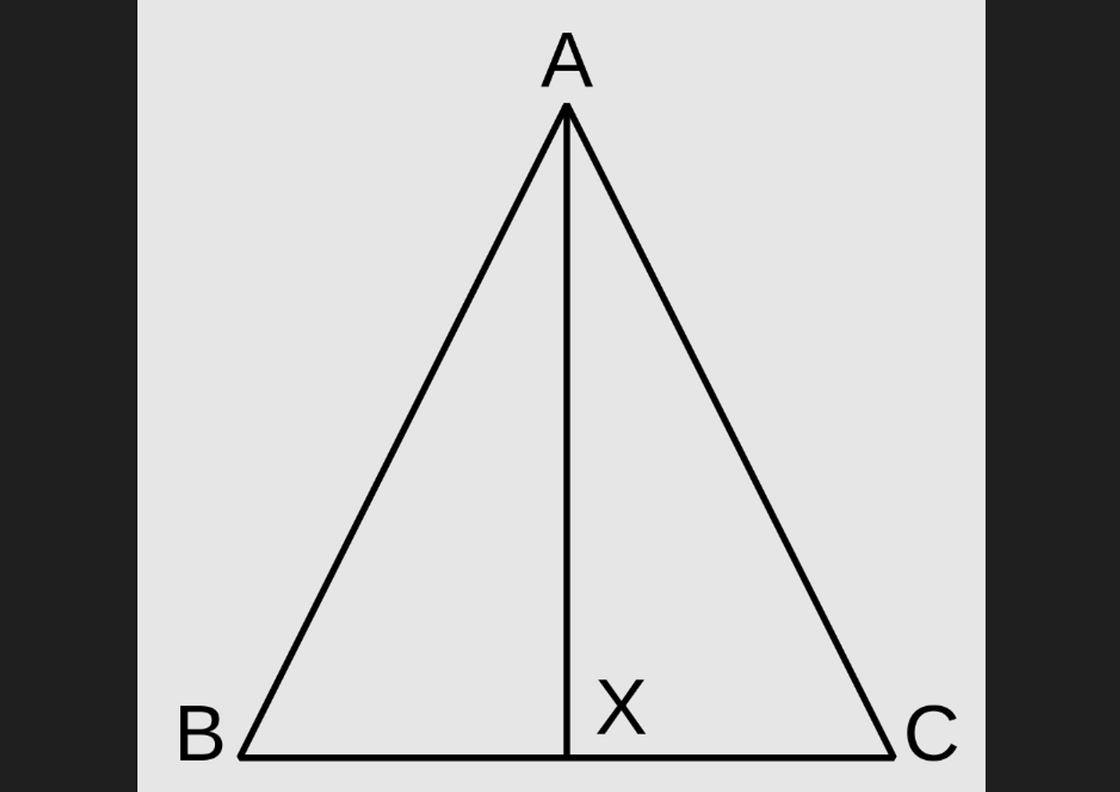
Как доказать, что треугольник равнобедренный? Пусть в треугольнике АВС (с вершиной А) сторона АВ=АС. Из вершины А проведем биссектрису к стороне ВС, которая пересечет её в точке Х. Биссектриса АХ разделит треугольник АВС на два равных треугольника: ВАХ=САХ. В этих треугольниках:
Раз в треугольниках два угла равны, то равны и третьи углы: АБХ=АСХ. По теореме о равнобедренных треугольниках против равных углов лежат равные стороны, то есть треугольник АВС равнобедренный.
При вычислении различных параметров равнобедренного треугольника учитывают его особенности:
Такие особые свойства помогут вычислить периметр, площадь треугольника, найти его основание с помощью специальных формул.
Периметр треугольника равен сумме его сторон. Если равные стороны равнобедренного треугольника обозначить как а, основание как b, то периметр (Р) вычисляйте по формуле: Р=а+а+b или Р=2а+b.
Например: а=5 см, b=8 см, тогда Р=2×5+8=10+8=18. Ответ: Р=18 см.
Площадь — это пространство, занимаемое фигурой. Платформа для изучения математики Cue Math предлагает несколько вариантов вычислений. Как найти площадь равнобедренного треугольника? Это можно сделать разными способами: зная длину основания и высоту треугольника, с помощью теоремы Пифагора, с помощью тригонометрических функций.
Например: как определить площадь, если a=5 см, b=8 см. По теореме Пифагора a²=(b2)²+h². Отсюда находим h²=a²–(b/2)²=5²–4²=9, h=3 см. Теперь находим площадь: S=b/2×h=4×3=12 см². Ответ: S=12 см².
Крупнейшая образовательная платформа BY JU’S предлагает список формул для определения площади равнобедренного треугольника при разных исходных данных. Эти формулы разной сложности и для разных уровней средней школы.
Как найти основание равнобедренного треугольника? Это можно сделать, если известны площадь фигуры и её высота. Из формулы S=b/2×h (где b — основание, h — высота) находим b=(S×2)÷h.
Например, известно, что S=243 см², h=27 см, надо найти основание b: b=(S×2)÷h=243×2÷27=18 см. Ответ: основание равно 18 см.
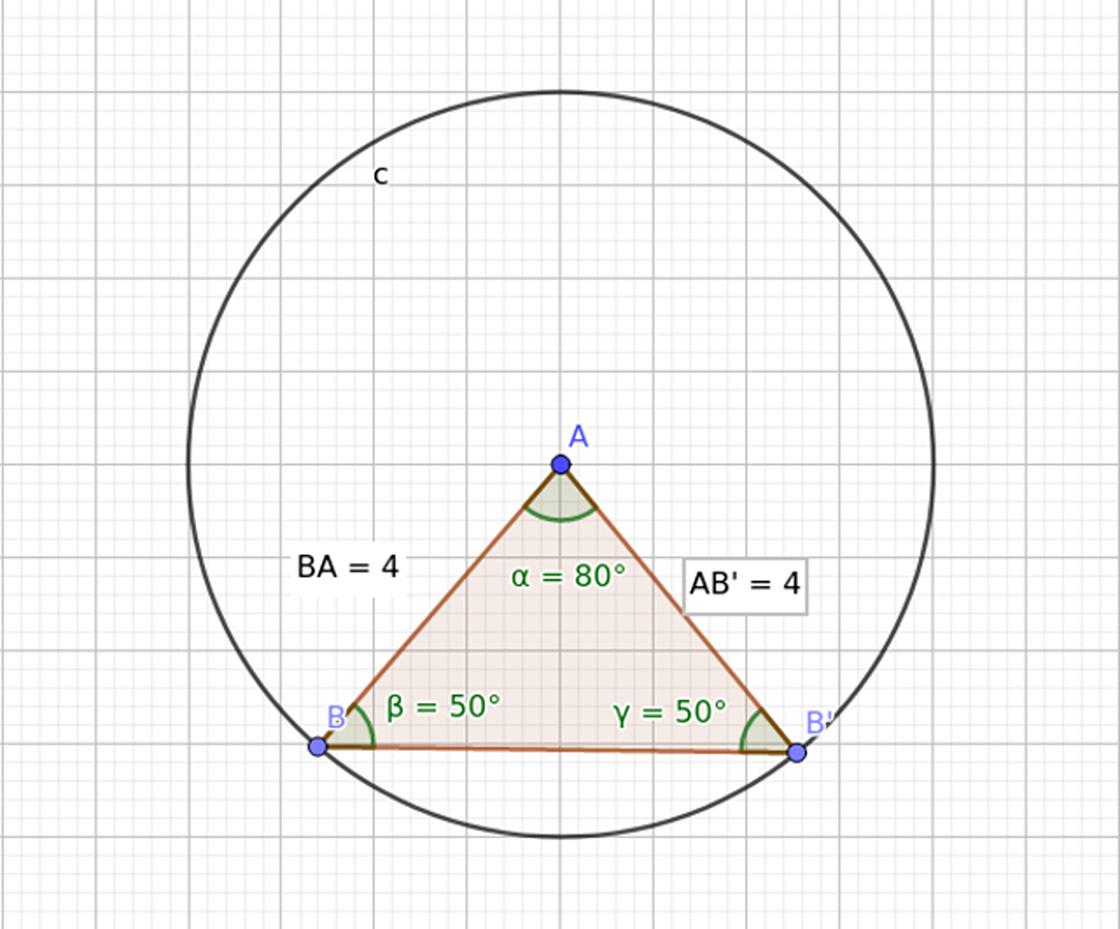
Равнобедренный треугольник — гармоничная геометрическая фигура. Формулы помогут определить различные её параметры.